INTÉGRATION ET MESURE

INTÉGRATION ET MESURE

La théorie de l’intégration joue en mathématique un rôle extrêmement important. C’est une théorie riche et complexe. Il ne sera pas question ici d’en donner une description exhaustive ni d’en aborder les assez redoutables aspects techniques. On s’efforcera de mettre en lumière les grandes idées simples qui y sont à l’œuvre et de montrer comment elles lient les aspects les plus élémentaires de la théorie de la mesure aux développements les plus généraux de la théorie de l’intégration.

1. Le problème initial Généralités

Mesurer est une activité dont l’existence est attestée dans toutes les sociétés historiques, et il est assez surprenant de constater que ce n’est que dans un passé relativement récent, au début du XX^e siècle, que la réflexion mathématique a commencé à en établir une théorie claire et cohérente.

Il faut tout de suite remarquer que le problème, pris dans sa plus grande généralité, reste encore mystérieux: on ne sait pas encore très clairement, par exemple, le sens qu’il faut donner au mot «mesurer», ni même si on peut vraiment lui donner un sens dans le domaine des sciences humaines, bien qu’on ait l’impression qu’une bonne conception de la mesure puisse y être l’origine de progrès décisifs.

Il faut encore remarquer que le mot «mesure» a, en mathématique, un sens plus restreint qu’en physique, et que ce que le mathématicien appelle théorie de la mesure ne s’applique directement qu’à une partie de l’activité du physicien et ne vise que la structure conceptuelle à l’exclusion des procédés expérimentaux de détermination des valeurs numériques qui relèvent de la métrologie.

Ce qui a retardé la naissance d’une bonne théorie de la mesure a été l’incapacité où est demeurée longtemps l’humanité de distinguer nettement entre ce que l’on mesure d’une part et l’échelle avec laquelle on mesure d’autre part, et de concevoir clairement ce qui les lie. L’échelle est constituée par le corps ordonné R des nombres réels (cf. nombres RÉELS), dont la théorie définitive n’a été élaborée qu’à la fin du XIX^e siècle (G. Cantor, R. Dedekind), mais qui avait été déjà presque totalement construit par le mathématicien grec Eudoxe, au IV^e siècle avant J.-C., sous le nom, que la tradition a conservé, de mesure des grandeurs (et de rapports de grandeurs), qui est révélateur de la confusion signalée plus haut. En réalité, Eudoxe ne considérait que ce que nous appelons les nombres réels positifs. Il le faisait d’une manière rigoureusement correcte et extrêmement pure: il est émouvant pour le mathématicien contemporain de constater le souci, très moderne, qu’a montré Eudoxe de ne rien introduire qu’il ne puisse construire par combinaison de concepts préalablement bien délimités. Mais sa construction, impeccable au point de vue de la rigueur, en ce qui concerne l’édification d’une échelle de valeurs, était beaucoup moins claire en ce qui concerne les «grandeurs». Elle était en outre d’une complexité qui l’a rendue inutilisable pour la plupart de ses successeurs; ceux-ci ne l’ont pas comprise et n’en ont retenu que des bribes, qu’ils se sont transmises avec une telle persévérance qu’on les trouve encore à l’état de vestiges peu intelligibles dans la plupart des manuels élémentaires. Ce qui a manqué à Eudoxe, c’est une autre idée très moderne qui consiste, lorsque l’on a construit, à partir d’un matériel conceptuel initial, de nouveaux êtres mathématiques très complexes par rapport aux éléments initiaux, à considérer les propriétés essentielles de ces nouveaux êtres et à repartir en les prenant à leur tour comme éléments initiaux d’une nouvelle construction. Dans la construction d’Eudoxe, comme dans celle de Dedekind, un réel apparaît comme un ensemble de rationnels, chaque rationnel étant lui-même un ensemble de couples d’entiers; mais Eudoxe reste fidèle au langage des entiers, tandis que Dedekind dégage explicitement la structure du corps totalement ordonné archimédien et complet des réels. (À noter d’ailleurs que l’axiome dit d’Archimède est explicitement attribué à Eudoxe par Archimède lui-même.)

C’est l’apparition presque simultanée d’une bonne théorie des nombres réels et de la notion d’ensemble qui a créé les conditions favorables à la naissance de la théorie moderne de la mesure.

Formulation de la question

Reprenons la question dans un cas simple: tout le monde a appris à calculer la surface ou l’aire de certaines régions du plan, et les mathématiciens des siècles passés ont consacré beaucoup d’efforts à calculer les aires de régions de plus en plus compliquées, sans jamais cependant dire très explicitement pourquoi ils menaient leurs calculs comme ils le faisaient, ni ce qu’ils attendaient du résultat. Expliciter les idées non formulées qui présidaient à ces recherches n’eut pas pour seul effet de satisfaire les exigences de rigueur et d’esthétique du mathématicien, cela lui permit de forger les outils propres à déterminer, puis à étendre le domaine de validité de ces calculs et de les effectuer dans tous les cas où ils sont valables.

Qu’attendons-nous en effet de ces calculs d’aire? Ils permettent (une unité d’aire étant choisie) d’attribuer à chaque région du plan d’un certain type un nombre réel positif que l’on appelle son aire, la propriété essentielle étant souvent exprimée par le fait que l’on peut «ajouter» des aires, ce que l’on peut décrire sous une première forme en disant que, si une région R apparaît comme formée de deux régions R¹ et R² «qui n’empiètent pas l’une sur l’autre», l’aire de R est la somme des aires de R¹ et de R². Deux régions telles que l’on puisse les «transporter» (au moins idéalement) l’une sur l’autre ont des aires égales.

Si l’on veut préciser ces idées, il faut d’abord savoir ce que l’on entend par «région» du plan. Le plan étant considéré comme un ensemble dont les éléments sont les points, le projet le plus ambitieux sera de considérer que tout sous-ensemble du plan doit avoir une aire. Cela signifierait donc que l’on peut définir une application m (appelée mesure universelle) de l’ensemble 戮( 刺) de toutes les parties du plan 刺 dans l’ensemble des nombres réels positifs, et que cette application a les propriétés d’additivité et d’invariance par isométrie.

Additivité. Pour tout couple (A, B) de parties disjointes du plan (c’est-à-dire telles que A 惡 B = 歷), on a:

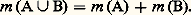Cette condition peut être également formulée sous la forme équivalente suivante:

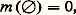et alors, pour tout couple de parties (A, B), du plan:

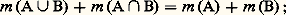ce qui permet de préciser le sens de «ne pas empiéter l’un sur l’autre» par «avoir une intersection d’aire nulle».

Invariance par isométrie. Quelle que soit la partie A du plan, et quelle que soit l’isométrie 精 du plan (une isométrie est une bijection du plan sur le plan qui conserve la distance), on a:

Cette définition précise étant donnée, deux problèmes se posent: Existe-t-il de telles applications? Si oui, en existe-t-il une seule, ou plusieurs? Il est clair que, s’il en existe une, que nous appellerons m , et, si est un réel positif fixe,m en est une autre. L’unicité recherchée ne sera donc qu’une unicité à un facteur près. Cela dit, la réponse aux questions posées est si peu évidente qu’on a, en réalité, les résultats suivants. Il existe une telle application dans le cas du plan, mais l’unicité n’est pas assurée. Il n’existe pas de telle application dans l’espace euclidien à trois dimensions (où l’on parle alors de volume et non plus d’aire), ni pour les espaces euclidiens à plus de trois dimensions (cf. S. BANACH).

Espaces mesurés

La non-existence ou la non-unicité amènent à restreindre nos ambitions initiales et à reposer le problème en essayant de définir l’application non pas sur l’ensemble de toutes les parties du plan ou de l’espace, mais sur un sous-ensemble. Pour donner une formulation plus générale, nous allons abandonner le plan et supposer que l’on part d’un ensemble X quelconque: Sur quelles parties 遼 de 戮(X) est-il raisonnable de chercher à définir une application additive?

Une première exigence est que, si A et B sont deux parties disjointes de X qui appartiennent à 遼, leur réunion appartient aussi à 遼. Mais il est plus commode d’exiger que, quelles que soient les parties A et B éléments de 遼, alors A 聆 B soit aussi élément de 遼. L’ensemble A 聆 B est d’autre part la réunion de A et de B 漣 A, qui sont disjoints, et il est commode que B 漣 A appartienne aussi à 遼.

Ce qui s’est effectivement révélé être la bonne structure pour l’ensemble 遼 est exprimé par la condition suivante: Pour tout couple (A, B) d’éléments de 遼, alors A 聆 B et A 漣 B sont éléments de 遼. (On peut montrer que cette condition est équivalente au fait que la différence symétrique A 蓮 B et l’intersection A 惡 B sont éléments de 遼, si A et B le sont.) On dit alors que 遼 est un clan de parties de X, ou quelquefois un anneau de Boole (face=F0021 遼 a une structure d’anneau pour les opérations 蓮 et 惡 (cf. ANNEAUX ET ALGÈBRES, chap. 2).

On dira alors qu’une application additive m de 遼 dans l’ensemble R⁺ des nombres réels positifs est une mesure (en précisant, si besoin est, simplement additive) ou encore une étendue (content , Inhalt ). La situation fondamentale est le triplet (X, face=F0021 遼, m ), où 遼 est un clan de parties de X, et m une application additive de 遼 dans R⁺. Un tel triplet est souvent appelé un espace mesuré .

Dans certains cas, il peut être intéressant (comme dans le cas de l’aire et du volume) d’avoir une propriété d’invariance par rapport à un sous-groupe G du groupe des bijections de X sur X, ce qui signifie que, pour tout g 捻 G et tout A 捻 遼, on a g (A) 捻 遼 et m [g (A)] = m (A), mais la théorie ne se limite pas à ce cas.

L’exemple le plus ancien d’espace mesuré qui ait été considéré par l’humanité est celui où X est un ensemble, 遼 l’ensemble de ses parties finies, et m (A) le nombre d’éléments de la partie finie A, et l’on peut dire que c’est à partir de ce cas, par extensions successives, qu’a été développée toute la théorie de la mesure.

Notons que, l’intersection d’une famille de clans étant un clan, il existe toujours un plus petit clan contenant une partie donnée de 戮(X): on dit alors que ce clan est engendré par la partie. On peut montrer qu’il existe des mesures non triviales (c’est-à-dire ne prenant pas uniquement la valeur 0) sur tout clan.

Voici des exemples usuels et importants d’espaces mesurés.

(a ) X = R, et 遼 est l’ensemble des réunions finies de semi-segments [a , b [ (a 諒 x 麗 b ), avec m ([a , b [) = b 漣 a . Il y a invariance par rapport aux translations de R. Cette mesure n’est autre que la longueur. On notera qu’il est préférable de considérer la longueur comme une application de 遼 dans R⁺, plutôt que de parler de la mesure de la longueur, qui, ou bien est un pléonasme, ou bien se réfère à un concept de longueur défini indépendamment, ce qui complique inutilement la situation.

(b ) X est un segment [ 見, 廓] de la droite, et 遼 est le clan engendré par les semi-segments [a , b [ et les segments [a , 廓]. On définit m au moyen d’une fonction positive croissante g définie sur [ 見, 廓] en posant m ([a , x [) = g (x ) et m ([ 見, 廓]) = g ( 廓). On peut interpréter m comme une masse. Si g n’est pas affine, cette masse m n’est pas «uniformément répartie».

(c ) X est le plan et 遼 est l’ensemble des réunions finies de rectangles dont les côtés ont des directions fixes, et la mesure d’un rectangle est le produit des longueurs de ses côtés. Il y a invariance par rapport au groupe des translations du plan.

(d ) X est un ensemble d’éventualités, 遼 un clan d’événements, avec X 捻 遼, et m une probabilité, à qui est imposée la condition m (X) = 1.

Les exemples les plus classiques représentés par ce schéma concernent, comme ci-dessus, les longueurs, les aires, les volumes, les masses et les probabilités: l’inclusion de la théorie des probabilités dans la théorie de la mesure (A. Kolmogoroff) a été l’origine du développement moderne de la première et d’un considérable enrichissement de la seconde (cf. calcul des PROBABILITÉS).

Extension d’une mesure

La formulation moderne du problème que les mathématiciens s’efforçaient de résoudre en calculant les mesures d’ensembles de plus en plus complexes est la suivante: Étant donné un espace mesuré (X, face=F0021 遼, m ), est-il possible de déterminer d’autres triplets (X, face=F0021 遼, m ), où 遼 說 遼 et où m est une extension de m à 遼?

L’idée d’une solution remonte-t-elle aussi à Eudoxe? Soit A une partie de X n’appartenant pas à 遼, mais telle qu’il existe au moins un élément 廓 捻 遼 avec A 說 廓. On considère alors tous les éléments 見 捻 遼 tels que 見 說 A (il en existe: il y a au moins l’ensemble vide) et tous les éléments 廓 捻 遼 tels que A 說 廓. On a donc:

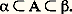Or, m étant additive et positive, m est croissante (c’est-à-dire que 見 說 廓 entraîne m ( 見) 諒 m ( 廓)). On en déduit alors que la borne supérieure de l’ensemble des nombres m ( 見) est au plus égale à la borne inférieure de l’ensemble des nombres m ( 廓). L’idée est que l’on pourra étendre m aux ensembles pour lesquels ces deux bornes sont égales, et le résultat qui justifie tous les calculs classiques est le suivant: La famille des ensembles A pour lesquels la borne supérieure des m ( 見) et la borne inférieure des m ( 廓) sont égales est un clan 遼 qui contient 遼, et, en posant:

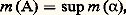on obtient une mesure sur 遼 dont la restriction à 遼 est m . En général, 遼 est strictement inclus dans 戮(X), et l’application du même procédé à (X, face=F0021 遼, m ) redonnerait le même triplet.

Dans le cas des aires planes, partant de l’espace mesuré de l’exemple (c ), on trouve tous les ensembles qualifiés classiquement de quarrables , et l’espace mesuré est invariant pour les isométries du plan: on obtient l’aire classique la plus générale.

2. Linéarisation et intégrale de Riemann

Soit (X, face=F0021 遼, m ) un espace mesuré. À chaque élément A de 遼, associons sa fonction caractéristique 﨏^A et considérons les combinaisons linéaires à coefficients réels de ces fonctions caractéristiques: on obtient des fonctions dites étagées (relativement à 遼) et leur ensemble V a une structure naturelle d’espace vectoriel réticulé. Si 﨏 et 祥 en sont deux éléments de V, sup( 﨏, 祥) et inf( 﨏, 祥) appartiennent aussi à V.

On peut alors associer à m une forme linéaire I sur V, en posant:

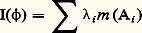pour:

et l’on vérifie que, si 﨏 s’exprime de deux manières différentes comme combinaisons linéraires de fonctions 﨏^Ai , on obtient bien, dans les deux cas, la même valeur pour I( 﨏). La linéarité de I est évidente. En outre, si 﨏 閭 0, on a I( 﨏) 閭 0.

On peut alors poser un problème d’extension de la forme I à un espace vectoriel contenant V. Le procédé classique de l’intégration de Riemann est l’analogue du procédé d’Eudoxe pour l’extension des mesures et peut être ainsi décrit. On considère les fonctions f définies sur X à valeurs dans R, qui ont la propriété d’être bornées et de s’annuler hors d’un ensemble A^f 捻 遼. On peut encadrer f par des fonctions étagées 﨏 et 祥 telles que 﨏 麗 f 麗 祥. On a donc: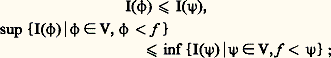

on montre que l’ensemble des fonctions pour lesquelles l’égalité a lieu dans la formule précédente est un espace vectoriel réticulé V qui contient V, et que, si l’on prend pour I(f ) la valeur commune aux deux bornes, on définit sur V une forme linéaire positive I qui prolonge I.

Tel est l’essentiel de l’intégration au sens de Riemann. Remarquons que, partant de (X, face=F0021 遼, m ), la famille des ensembles A dont les fonctions caractéristiques 﨏 appartiennent à V n’est autre que 遼, et que I( 﨏) n’est alors autre que m (A). On ne perd donc rien, et on gagne beaucoup à procéder à cette linéarisation et à travailler sur des espaces vectoriels de fonctions et sur leurs formes linéraires positives.

Un problème technique concernant cette intégration est de savoir, suivant l’espace mesuré (X, face=F0021 遼, m ), ou l’espace V, dont on part, si l’on peut caractériser indépendamment de l’intégration les fonctions de V: dans cet ordre d’idées, si X est localement compact, et si 遼 contient tous les compacts de X, toutes les fonctions continues à support compact appartiennent à V. Plus particulièrement, si (X, face=F0021 遼, m ) est l’espace mesuré de l’exemple (b ), où m est définie à partir d’une fonction croissante g , toutes les fonctions continues réelles sur [ 見, 廓] sont intégrables, et l’intégrale est appelée l’intégrale de Riemann-Stieltjes par rapport à g et est souvent notée:

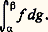Une fonction v à variation bornée étant la différence de deux fonctions croissantes p et n , on peut définir l’intégrale de toute fonction continue f par rapport à v en posant:

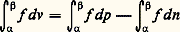et on a: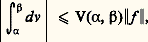

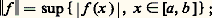où 瑩f 瑩 est la norme uniforme de f , définie par:

V( 見, 廓) est la variation absolue de v entre 見 et 廓, soit:

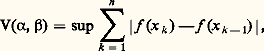où la borne supérieure est prise par rapport à l’ensemble des subdivisions finies 見 = x ⁰ 麗 x ¹ 麗 ... 麗 x ^n-1 麗 x ⁿ = 廓 de l’intervalle [ 見, 廓].

Autrement dit, sur l’espace de Banach des fonctions continues réelles définies sur [ 見, 廓], les intégrales de Riemann-Stieltjes sont des formes linéaires continues. En 1909, F. Riesz a prouvé qu’elles étaient les seules.

3. La théorie de Lebesgue

L’additivité dénombrable

On s’est efforcé, dans ce qui précède, de mettre en lumière les idées implicites essentielles de la théorie classique de la mesure et de l’intégration telle qu’elle s’est développée non sans difficultés des Grecs à Riemann, et qui constitue ce que l’on peut appeler la théorie élémentaire de la mesure.

Mais, historiquement, cette prise de conscience de ce qui intervenait fondamentalement dans la théorie classique s’est produite en même temps, sinon plus tard que l’introduction d’une nouvelle idée extrêmement féconde, due à É. Borel, et qui est celle de l’additivité dénombrable.

Reprenons un triplet (X, face=F0021 龍, p ), et supposons que le clan 龍 contient non seulement les réunions finies de ses éléments, mais aussi les réunions dénombrables, c’est-à-dire supposons que la réunion de toute famille dénombrable d’éléments de 龍 soit un élément de 龍. On dit alors que 龍 est une tribu , ou encore un 靖-anneau (de Boole).

Supposons que 猪 soit non seulement additive, mais vérifie la condition suivante: Pour toute famille dénombrable (Aⁱ ), i 捻 N d’éléments de 龍 deux à deux disjoints, on a:

on dit alors que 猪 est dénombrablement additive (ou 靖-additive). C’est cette situation qui a été envisagée par Borel et qui est toujours, sauf précision limitative, désignée par le terme espace mesuré .

Un premier problème est celui de l’existence de tels triplets. Il est évident qu’il existe des tribus: pour tout ensemble X, l’ensemble 戮(X) de ses parties est une tribu. De plus, l’intersection de toute famille de tribus étant une tribu, il existe, pour toute partie 暈 de 戮(X), une plus petite tribu qui la contient; on appelle cette dernière la tribu engendrée par 暈.

L’existence d’une mesure 靖-additive a posé un problème plus redoutable, qui a été résolu par Lebesgue suivant une voie que l’on peut schématiser, dans un cadre plus général que le sien, de la façon suivante: Partons d’un triplet (X, face=F0021 遼, m ), où 遼 est un clan et m une mesure simplement additive, et considérons la famille D(face=F0021 遼) des parties A de X telle que chacune de ces parties soit incluse dans la réunion d’une famille dénombrable ( 見ⁱ ), i 捻 N, d’éléments de 遼. On peut considérer la somme: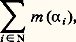

qui est un réel positif ou + 秊, et désigner par m (A) la borne inférieure de l’ensemble de ces sommes obtenues en considérant toutes les familles dénombrables d’éléments de 遼 dont la réunion contient A. L’idée est que m (A) doit fournir une approximation par le haut (en langage plus mathématique, un majorant) de l’éventuelle mesure de A. On définit ainsi une application m de D(face=F0021 遼) dans R 漣⁺ (union de R⁺ et de+ 秊參). Il est clair qu’une réunion dénombrable d’éléments Aⁱ de D(face=F0021 遼) est un élément de D(face=F0021 遼) et l’on a:

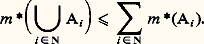Cette propriété, plus faible que la 靖-additivité, est appelée la 靖-sous-additivité, et m est qualifiée de mesure extérieure associée à (X, face=F0021 遼, m ).

On considère alors les éléments A de D(face=F0021 遼) tels que l’on ait, pour tout élément E de D(face=F0021 遼):

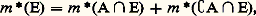et on montre que leur ensemble est une tribu 龍 qui contient 遼 et que la restriction 猪 de m à 龍 est 靖-additive. Les éléments de 龍 sont qualifiés d’ensembles mesurables , ou (face=F0021 遼, m )-mesurables si on veut rappeler leur origine.

Lebesgue a d’abord démontré ce résultat dans le cas où X est un segment de la droite, 遼 le clan engendré par les segments, et m la longueur. Le même processus peut être appliqué à la droite entière, et la mesure obtenue, qui prolonge la longueur et qui est invariante par translation, est appelée mesure de Lebesgue de la droite. (Le même procédé réussit pour les aires, les volumes et l’on parle encore de mesure de Lebesgue dans R², R³, Rⁿ .)

Il faut noter que 龍 est en général strictement incluse dans 戮(X) et on démontre par exemple, dans le cas de la droite, qu’il est impossible d’étendre la mesure de Lebesgue à 戮(X) tout entier.

La tribu 龍 dépend de 遼 et de m , mais 龍 contient toujours la plus petite tribu contenant 遼. En particulier, dans le cas de Rⁿ , la tribu des ensembles mesurables au sens de Lebesgue (face=F0021 遼 étant le clan engendré par les produits d’intervalles bornés, appelés pavés , et m le volume n -dimensionnel) contient la tribu engendrée par les pavés, qu’on appelle tribu borélienne de Rⁿ , elle contient tous les ouverts et tous les fermés de Rⁿ . (Ses éléments sont appelés boréliens de Rⁿ .)

Dans tous les cas, la tribu 龍 est complète par rapport à 猪, en ce sens que, si A 捻 龍 avec 猪(A) = 0, toute partie de A appartient aussi à 龍 et a aussi une mesure nulle. Le triplet (X, face=F0021 龍, 猪) a été construit à partir du triplet (X, face=F0021 遼, m ) et on a 遼 說 龍; 猪 est-elle une extension de m ? En général, on a seulement pour 見 捻 遼:

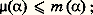l’égalité est assurée pour tout 見 捻 遼, si et seulement si, pour tout élément 見 de 遼 qui est réunion d’une famille dénombrable d’éléments deux à deux disjoints 見ⁱ , de 遼, on a:

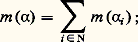c’est ce qui est réalisé pour les longueurs, les aires, les volumes...

L’intégrale de Lebesgue

En même temps qu’il démontrait l’existence de mesures 靖-additives, Lebesgue définissait l’intégrale qui porte son nom.

Dans le cas simple de fonctions réelles bornées nulles hors d’un élément de 龍 de mesure finie, le processus indiqué pour l’intégrale de Riemann conduit, à condition de partir des fonctions étagées relatives à (X, face=F0021 龍, 猪), à l’intégrale de Lebesgue. Les fonctions bornées nulles hors d’un ensemble mesurable de mesure finie qui sont intégrables sont alors exactement celles que Lebesgue a appelées mesurables, c’est-à-dire celles qui donnent pour image réciproque de tout borélien de R un ensemble mesurable (c’est-à-dire appartenant à 龍). Signalons en passant que cette notion de fonction mesurable (dont la dénomination n’est d’ailleurs pas heureuse) est très importante et se définit de façon générale dans la situation suivante: face=F0021 遼 étant une tribu de parties d’un ensemble X, et 龍 une tribu de parties d’un ensemble 﨏, une application f de X dans 﨏 est dite (face=F0021 遼, 龍)-mesurable si l’image réciproque de tout élément de 龍 est un élément de 遼. Si une mesure 猪 a été définie sur 遼, cela permet d’en définir une 益 sur 龍, en posant, pour tout B 捻 龍:

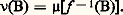Pour les fonctions bornées, la différence essentielle entre l’intégration de Riemann et celle de Lebesgue réside dans le fait que la première part d’un clan et d’une mesure simplement additive et la seconde d’une tribu et d’une mesure 靖-additive, fait qui avait été obscurci par certains commentaires déclarant que, dans le cas de fonctions réelles définies sur un segment de R, Riemann partageait le domaine de la variable et Lebesgue celui de la fonction, ce qui ne correspondait qu’à deux manières d’obtenir des fonctions étagées (que ni l’un ni l’autre n’utilisaient explicitement).

Lebesgue ne se limitait en outre pas aux fonctions bornées ou définies sur des ensembles de mesure finie, mais il étendait son intégrale de telle sorte qu’elle apparaissait finalement comme une forme linéaire positive I, classiquement notée:

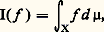sur l’espace 硫¹, ou, si l’on veut préciser, 硫¹(X, face=F0021 龍, 猪), des fonctions intégrables qui est un espace vectoriel réticulé, avec les propriétés suivantes:

(a ) f 捻 硫¹ est équivalent à |f | 捻 硫¹.

(b ) Sur 硫¹, I(|f |) est une semi-norme. La relation:

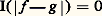est équivalente, du fait que f et g prennent les mêmes valeurs sauf aux points d’un ensemble de mesure nulle, ce que l’on traduit en disant qu’elles sont égales presque partout . L’égalité presque partout est une relation d’équivalence, et l’espace quotient est un espace vectoriel normé, classiquement noté L¹(X, face=F0021 龍, 猪) qui a la remarquable propriété d’être complet.

(c ) Si f ⁿ est une suite croissante de fonctions intégrables, telles que la suite I(f ⁿ ) converge, la suite f ⁿ converge simplement presque partout (c’est-à-dire sauf aux points d’un ensemble de mesure nulle) vers une fonction intégrable f telle que:

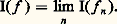(d ) Théorème de la convergence dominée . Si une suite de fonctions intégrables f ⁿ converge presque partout vers une fonction f et s’il existe une fonction intégrable g telle que, pour tout n 捻 N, on ait |f ⁿ | 諒 g , alors f est intégrable et:

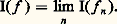4. L’intégrale comme forme linéaire

Le fait que l’intégrale est une forme linéaire sur un espace vectoriel de fonctions est si fondamental qu’il peut en constituer une définition; cependant cette importance n’était pas encore perçue au moment où Lebesgue créait son intégrale. Un des résultats qui contribua le plus à dégager le rôle de cette notion fut le théorème de F. Riesz, déjà cité, sur l’identité entre les intégrales de Stieltjes des fonctions continues réelles définies sur un segment [a , b ] et les formes linéaires continues sur l’espace de Banach que constituent ces fonctions. Les idées de Riesz furent étendues par J. Radon, dont le nom est désormais associé aux formes linéaires continues sur l’espace V des fonctions continues à support compact définies sur un espace localement compact X, l’espace V étant muni de la topologie de la convergence compacte; l’hypothèse de continuité que l’on impose ici à une forme linéaire m sur V s’exprime par le fait que, pour tout compact K de X, il existe une constante M(K) telle que:

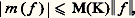où: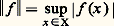

pour toute fonction f 捻 V nulle en dehors de K. L’aspect linéaire a paru tellement important aux mathématiciens contemporains, et en particulier à Bourbaki, qu’ils utilisent le terme de mesure de Radon pour désigner non plus des fonctions 靖-additives d’ensembles, mais les formes linéaires décrites ci-dessus.

Un autre pas en direction de la linéarisation fut accompli par l’Américain P. J. Daniell, qui exposa une théorie de l’intégration comme méthode de prolongement d’une forme linéaire positive présentant une «continuité» convenable.

Une théorie de l’intégration est d’abord l’étude du prolongement d’une forme linéaire, continue en un certain sens, sur un espace vectoriel de fonction à un espace vectoriel plus vaste. Le cœur de la question est que cet espace plus vaste se présente naturellement sous deux formes différentes – comme complété d’un espace vectoriel topologique dont les éléments sont a priori des classes d’équivalence de suites de Cauchy (cf. espaces MÉTRIQUES, espaces vectoriels NORMÉS), ou comme quotient, relativement à une relation d’égalité presque partout, d’espaces de fonctions) – dont il s’agit de montrer qu’elles sont isomorphes.

Voici le schéma d’une telle théorie (selon M. H. Stone).

(a ) Le départ est un espace vectoriel V réticulé d’applications d’un ensemble X dans R, contenant inf(1, f ) s’il contient f , et une forme linéaire positive I sur V telle que:

(b ) Cela étant, on associe à toute application f de X dans R la quantité N(f ) (réelle positive ou égale à + 秊) définie par: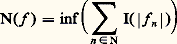

où la borne inférieure est prise par rapport à l’ensemble des suites (f ⁿ ) de fonctions de V telles que:

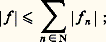on a alors:

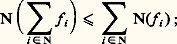on se restreint alors à l’ensemble G des fonctions f pour lesquelles N(f ) est fini . L’ensemble G est un espace vectoriel qui contient V et sur lequel N est une semi-norme.

Le résultat essentiel est que G est complet pour cette semi-norme.

(c ) On considère alors l’adhérence V de V dans G qui est un espace complet pour la semi-norme N; on peut prolonger de manière unique, par continuité, I en une forme linéaire 壟 continue (relativement à N) sur V. Puisque 壟 s’annule sur le sous-espace des fonctions telles que N(f ) = 0, on peut définir une forme J sur l’espace quotient 律 de V pour la relation d’équivalence N(f 漣 g ) = 0, et 律 est un espace de Banach. Si, comme c’est souvent le cas, N(f ) = 0 entraîne f = 0 si f 捻 V, V est isomorphe à un sous-espace de 律 et on peut considérer J comme le prolongement de I de V à 律.

壟 et V ont toutes les propriétés signalées plus haut pour l’intégrale de Lebesgue et les espaces 硫¹(X, face=F0021 龍, 猪); V est l’espace 硫¹(X, face=F0021 龍, 猪) pour la tribu 龍 engendrée par les ensembles E dont les fonctions caractéristiques appartiennent à V, avec 猪(E) = 壟(X^E). L’espace 律 correspond à L¹(X, face=F0021 龍, 猪) et J est la forme déduite de l’intégrale par le passage au quotient.

Une situation extrêmement importante déjà signalée, mais qui entre dans ce cadre général, est le cas où V est l’espace des fonctions réelles continues à support compact définies sur un espace localement compact et où I est une forme linéaire continue sur V muni de la topologie de la convergence compacte, c’est-à-dire le cas des mesures de Radon, qui s’expriment comme différences de deux formes positives.

Enfin signalons, sans donner le moindre détail, qu’il est possible de définir, en en conservant la linéarité et une continuité convenablement définie, des intégrales à valeurs non plus seulement réelles, mais dans C, dans Rⁿ et plus généralement dans les espaces vectoriels topologiques localement convexes.

Espace L^p

Aux espaces 硫¹ et L¹(X, face=F0021 龍, 猪) peuvent être associés d’autres espaces remarquables, dont une des définitions peut être présentée comme suit: Appelant mesurables les fonctions réelles, qui sont (face=F0021 龍, B)-mesurables, où B est la tribu borélienne de R, l’espace 硫^p pour p 閭 1, est constitué des fonctions mesurables telles que |f |^p 捻 硫¹. C’est un espace vectoriel sur lequel N^p définie par:

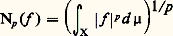est une semi-norme. La relation N^p (f ) = 0 est équivalente à l’égalité presque partout, et l’espace quotient relativement à cette relation, L^p (X, face=F0021 龍, 猪), est normé et complet.

De plus, si p 1, le dual topologique de L^p est isomorphe à L^q si: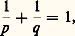

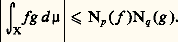et on a l’inégalité dite de Hölder, pour f 捻 L^p et g 捻 L^q :

Pour p = 2, on a q = 2 et l’espace L² est isomorphe à son dual topologique. L’inégalité de Hölder prend la forme particulière appelée inégalité de Schwarz:

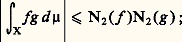戀

咽Xfg d 猪 ne dépend que des classes de f et de g et permet de définir un produit scalaire sur L² qui apparaît alors comme un espace de Hilbert et joue un rôle extrêmement important en analyse harmonique et en physique quantique.

On désigne par 硫 秊 l’espace des fonctions mesurables bornées presque partout. C’est un espace vectoriel sur lequel on peut définir une semi-norme N size=1^秊(f ), égale au plus petit réel positif k tel que l’ensemble:

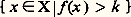soit de mesure nulle. L’espace quotient, relativement à l’égalité presque partout, est noté L 秊. Il est normé et complet. Il est isomorphe au dual topologique de L¹, mais il n’y a pas cette fois réciprocité, le dual de L 秊 contient au moins un sous-espace isomorphe à L¹, mais le contient strictement.

Mesure de Haar

La longueur, l’aire, le volume sont des mesures de Radon invariantes par les translations de R, R², R³.

Un résultat très général et très important, dû à Haar, généralise cette situation: Soit G un groupe topologique localement compact, dont l’opération est notée multiplicativement. Si s est un élément du groupe, à toute fonction continue à support compact f on peut associer la fonction f ^s , également continue à support compact, définie par:

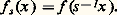Le théorème de Haar affirme qu’il existe alors une mesure de Radon sur G unique (à un facteur près) invariante à gauche , c’est-à-dire telle que, pour tout s 捻 G et pour toute fonction f ,

5. Intégration et dérivation

Un très célèbre théorème d’analyse classique énonce que, si f est une fonction continue réelle définie sur [a , b ], l’application:

est dérivable et admet f (x ) pour dérivée au point x .

En vertu de ce théorème, intégration et dérivation sont souvent présentées comme des «opérations inverses» l’une de l’autre.

En réalité, la recherche des primitives (ce qui est vraiment l’inversion de la dérivation) et l’intégration ne coïncident nullement, car les fonctions intégrables ne sont pas toutes des fonctions dérivées, et les fonctions dérivées ne sont pas toutes intégrables.

Le problème de la recherche des primitives de la fonction dérivée la plus générale a été résolu par A. Denjoy dans sa belle et difficile théorie de la totalisation.

Mais le problème peut être présenté autrement: partant d’un espace mesuré (X, face=F0021 龍, 猪) et d’une fonction intégrable f , on peut définir une mesure 益 sur 龍, en prenant pour valeur 益(A) de la mesure d’un élément A de 龍 l’intégrale de f 﨑^A, où 﨑^A est la fonction caractéristique de A. Réciproquement, 益 étant une mesure sur 龍, existe-t-il une fonction intégrable f telle que, pour tout A 捻 龍, on ait: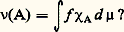

La réponse est fournie par le théorème de Radon-Nikodym (d’ailleurs énoncée et démontrée par Lebesgue dans le cas où 猪 est la mesure de Lebesgue sur R), que nous ne donnerons pas dans sa plus grande généralité: Si X 捻 龍 et 猪(X) 麗 + 秊, la condition nécessaire et suffisante pour que 益 puisse s’exprimer par:

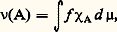est que, pour tout ensemble B de 龍,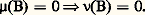

La fonction f n’est évidemment déterminée que presque partout, mais est unique à cela près, et peut être considérée comme une densité de la mesure 益 par rapport à la mesure 猪: c’est, en fait, la meilleure manière et la plus générale de concevoir la notion de densité.

Encyclopédie Universelle. 2012.